
Её величество Геометрия
Вся красота мира – в музыке, природе, архитектуре, поэзии, живописи, – имеет свои закономерности, описываемые математически. Две тысячи лет назад поиском этих закономерностей занимался Пифагор, древнегреческий учёный. Наука в те времена только зарождалась, вырастая из практических наблюдений и прикладных рекомендаций. Пифагор придал геометрии форму свободной науки, проводя свои исследования с нематериальной, интеллектуальной точки зрения. Пифагорейцы начали изучать свойства фигур с помощью логических доказательств, а не измерений. Умение наблюдать и видеть, строить чертежи и находить в них явленные закономерности и свойства фигур, – на этом и стоит вся геометрия. Как же прийти к ней, такой строгой, точной и красивой? Прийти так, чтобы строгость красоты не отпугивала, а радовала глаз и давала надёжную опору душе?
В вальдорфской школе этот путь к её величеству Геометрии начинается на первом уроке в первый учебный день первого класса. На этом уроке ребята рисуют прямую и кривую – две линии, из которых складывается всё многообразие форм. Первоклассники на уроках рисования форм учатся проводить эти линии чётко, уверенно, формы усложняются (рис. 1, 2) и к концу 1 класса в работах появляется вертикальная симметрия (рис. 3, 4). Мы живём в мире вертикальной симметрии – ею пронизаны живые существа, архитектура, растения… И ребёнок учится создавать отражение фигуры любой сложности.

|

|
| Рис. 1 | Рис. 2 |

|

|
| Рис. 3 | Рис. 4 |
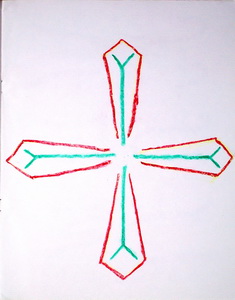
В конце 2 класса, когда жизнь ребёнка проходит в полярностях (добра и зла, басен и легенд о святых, земной тяжести и небесной лёгкости), добавляется горизонтальная симметрия (рис. 5, 6).

|

|
| Рис. 5 | Рис. 6 |
|
| Рис. 7 |
В третьем классе, когда ребёнок впервые в своей жизни обособился от мира и пришёл к себе как точке, некоему центру – появляется центральная симметрия, где надо согласовывать и верх с низом, и правую половину с левой (рис. 7). Дети рисуют метаморфозы фигур – череду рисунков, в которой на каждом следующем шаге происходит небольшое изменение фигуры (рис. 8).

|

|
| Рис. 8-1 | Рис. 8-2 |

|

|
| Рис. 8-3 | Рис. 8-4 |

|
|
| Рис. 8-5 | Рис. 8-6 |

|

|
| Рис. 8-7 | Рис. 8-8 |
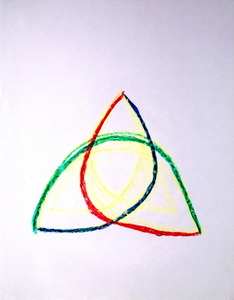
В 4 классе появляется возможность увидеть и нарисовать переплетение линий. Это ещё не объёмная фигура, но уже зачатки третьего измерения. В этом классе дети ткут, плетут и вышивают, поэтому такие формы, как правило, рисуются с большим удовольствием (рис. 9, 10).

|

|
| Рис. 9 | Рис. 10 |
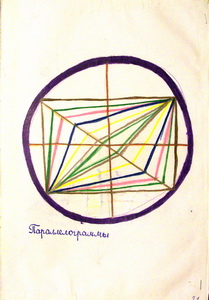
В 5 классе появляется предмет «геометрия свободной руки». Это уже геометрия, так как вводятся геометрические термины – названия фигур и их составляющих (рис. 11, 12), понятия перпендикулярности, параллельности, величины угла (рис. 13); рассматриваются отношения фигур, прямых и точек. Все чертежи в этом классе выполняются без инструментов, свободной рукой – и мы доводим свои руки до совершенства, строя чертежи и всевозможные «красивые формы» (рис. 14).
|

|
| Рис. 11 | Рис. 12 |

|

|
| Рис. 13 | Рис. 14 |
Наступает шестой класс. Мы берём инструменты. И тут возникает вопрос – если руки способны чертить окружности и прямые линии ровно, то зачем же нужны циркуль и линейка? Оказывается – для точности. Пришло время, когда точность построенного чертежа даёт возможность видеть геометрические закономерности, а способность видеть, в свою очередь, позволяет решать поставленные задачи. Так и строились уроки – сначала чертили основной чертёж, потом старались увидеть в нём всё, что можно – равенство отрезков и углов, перпендикулярность и параллельность, правильные фигуры и т.п. Затем получали задания – разделить пополам произвольный отрезок, угол или дугу; построить прямую, параллельную заданной; построить угол, равный заданному; построить треугольник с заданными сторонами – и всё это надо было делать исключительно с помощью циркуля и линейки. Каждое задание как собственное исследование, каждое решение – собственное открытие! Какие-то задачи решались за 5 минут, на другие уходил весь урок. Нередко в классе рождались 2 или 3 способа решения поставленной задачи – такие моменты всегда радуют явленным творчеством и работой мысли.
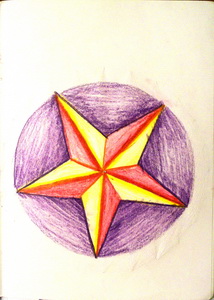
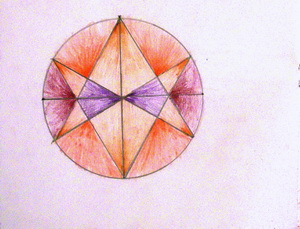
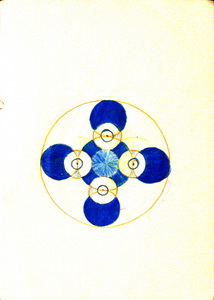
Кроме строгих чертежей, наблюдений и решений задач, было ещё и построение цветных чертежей, где раскрашивание создавало иллюзию объема фигуры (рис. 15, 16), демонстрировало разные подходы к игре цветов в чертеже (рис. 17, 18, 19).

|
|
| Рис. 15 | Рис. 16 |
|
|
| Рис. 17 | |

|
|
| Рис. 18 | Рис. 19 |
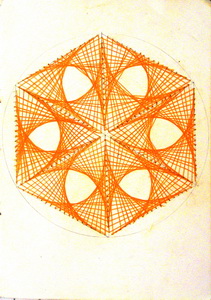
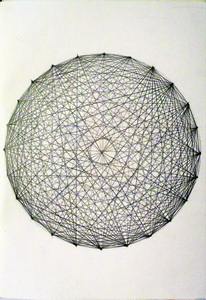
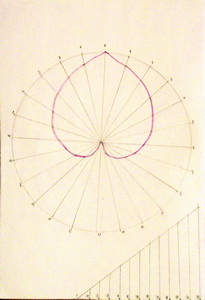
Были у нас и чертежи, красота которых могла быть достигнута только при абсолютной точности (рис. 20, 21). Один из них позже был воплощен нитками на бумаге – посредством изонити (рис. 22).
|
|
| Рис. 20 | Рис. 21 |

|
|
| Рис. 22 | |
|
|
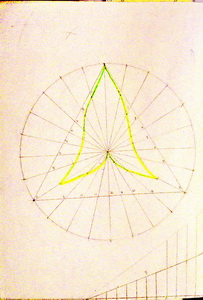
| Рис. 23 | Рис. 24 |
Наблюдения, самостоятельный поиск решения задачи, умение описать пошагово выполненное построение – качества, которые будут необходимы в следующих классах, где появятся теоремы и доказательства, более сложные построения. Самое важное при этом, на мой взгляд, уметь и дальше видеть красоту этой науки, её способность описать всё окружающее нас; уметь применять дары геометрии в творчестве, ведь в 7 классе нас ждёт знакомство, в частности, с перспективой и золотым сечением…











